The Stakes of the Mobile (4:7a-c) Grassmann III: The Body in the Diagram

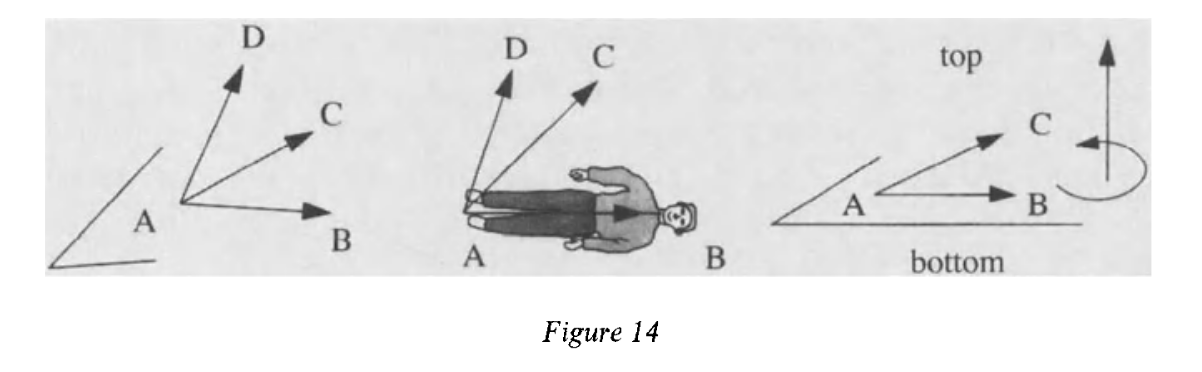
Section 7 of Châtelet’s chapter on Grassmann marks a shift to the generative power of multiplication. Pedagogically, the fundamentals are introduced through addition: gestural lines are chained together, extended, and loop back in the parallelogram. But with multiplication, we arrive at the parallelogram differently, not through one more operation but through a genuine rupture. Multiplication is no longer tied, as it has been historically, to addition. Instead, we have a wedge that fuses two gestures into a new category: the external as a leap into a new quality. And in so doing, (along with the insistence on the orientation of a body, even if virtually, within the diagram), Grassmann is able to fold intensive orientation into the process itself. The parallelogram maintains and expresses an antisymmetrical orientation. Its front and back are not equivalent. And it matters which way you go from here. 

This is also where we see, perhaps most clearly, Grassmann’s inclusion of the body in the process. (Which prompted more questions than it solved! Why does the body lie down? What are we to make of the oscillation between the body and its view? And how are we supposed to think of this sequencing of time through movement?) But it is more than just decorative or a kind of pedagogic aid. Rather, the pedagogic function of the body is inherent to the mathematical process itself. Lying the reader on AB to see AC is Châtelet’s way of making the emergence of dimension a physical experience that drives the intuition traced by the equation as a cohesive gesture. 

We have escaped the trap of the transitivity of trajectories. […] Here, it is the whole body that appropriates space. (128) 

And this move to a non-additive sense of multiplication highlights Grassmann’s commitment to naturphilosophie. The philosopher Baader had already seen this fundamental shift from discrete addition to a generative process: 

The world is not a collection of parts, a conglomerate of atoms, but an organic mass governed by a single principle. […] In other terms, there is no mechanical construction of the body as object occupying space …; and a principle other than the simple mechanism of nature is needed, not only for the constitution of organic bodies, but also for all bodies in general. (123) 

What Grassmann gives us here is a kind of intensive/extensive ladder for working with these living forces in math, exhausting the additive to the point where it feels inadequate, and introducing a wedge or liaison that expresses a multiplicative power that opens up new possibilities.